کارایی یک طبقهبندی کننده
بعد از پیادهسازی الگوریتم یادگیری ماشین، باید دریابیم که مدل چقدر مؤثر است. معیارهای سنجش اثربخشی ممکن است مبتنی بر دیتاست و متریک باشند. برای ارزیابی الگوریتمهای مختلف یادگیری ماشین، میتوان از معیارهای کارایی مختلف استفاده کرد. بهعنوانمثال فرض کنید اگر از یک طبقهبندی کننده برای تشخیص اشیاء تصاویر مختلف استفاده شود، میتوانیم از معیارهای کارایی طبقهبندی مانند دقت متوسط، AUC و غیره استفاده کنیم. به معنای دیگر متریکی که برای ارزیابی مدل یادگیری ماشین خود استفاده میکنیم بسیار مهم است، زیرا انتخاب معیارها (متریکها) بر نحوه اندازهگیری و مقایسه کارایی الگوریتم یادگیری ماشین تأثیر میگذارد. در ادامه برخی از این متریکها آمده است.
ماتریس درهمبرهم
در اصل از آن برای مسئله طبقهبندی استفاده میشود که در آن خروجی میتواند از دو یا چند کلاس باشد. این سادهترین روش برای اندازهگیریِ کارایی یک طبقهبندی کننده است. ماتریس درهمبرهم درواقع یک جدول با دو بعد یعنی “واقعی” و “پیشبینی” است. هر دو بُعد دارای “مثبت واقعی (TP)”[1]، “منفی واقعی (TN)”[2]، “مثبت کاذب (FP)”[3] و “منفی کاذب (FN)”[4] هستند.
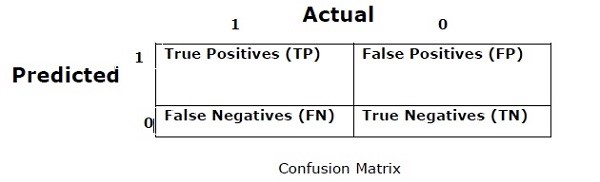
در ماتریس درهمبرهم بالا، 1 برای کلاس مثبت و 0 برای کلاس منفی است.
اصطلاحات مرتبط با ماتریس درهمبرهم در زیر آمده است:
مثبتهای واقعی – مواردی هستند که کلاس واقعی نقطه داده 1 بوده و پیشبینیشده نیز 1 است.
منفیهای واقعی – مواردی هستند که کلاس واقعی نقطه داده 0 بوده و پیشبینیشده نیز 0 است.
مثبتهای کاذب – مواردی هستند که کلاس واقعی نقطه داده 0 بوده و پیشبینیشده نیز 1 است.
منفیهای کاذب – مواردی هستند که کلاس واقعی نقطه داده 1 بوده و پیشبینیشده نیز 0 است.
دقت[5]
ماتریس درهمبرهم بهخودیخود معیار اندازهگیری کارایی نیست اما تقریباً تمام ماتریسهای کارایی بر اساس ماتریس درهمبرهم است. یکی از آنها ماتریس دقت است. در مسائل طبقهبندی، ممکن است بهعنوان تعداد پیشبینیهای درستِ ساختهشده از مدل نسبت به انواع پیشبینیهای انجامشده تعریف شود. فرمول محاسبه دقت به شرح زیر است –
$$Accuracy = \frac{TP TN}{TP FP FN TN}$$
صحت (درستی)
اغلب در بازیابی اسناد استفاده میشود. ممکن است بهعنوان این تعریف شود که چه تعداد از مدارک بازگشتی صحیح هستند.
برای محاسبه صحت، از فرمول زیر استفاده میکنیم –
$$Precision = \frac{TP}{TP FP}$$
یادآوری یا حساسیت
ممکن است نشاندهنده تعداد مثبتهایی باشد که مدل برمیگرداند. در زیر فرمول محاسبه یادآوری یا حساسیت مدل آمده است –
$$Recall = \frac{TP}{TP+FN}$$
اختصاصی[6]
ممکن است نشاندهنده تعداد منفیهایی باشد که مدل برمیگرداند. در زیر فرمول محاسبه اختصاصی مدل آمده است –
$$Specificity = \frac{TN}{TN+FP}$$
مسئله (مشکل عدم توازن کلاس)
عدم توازن کلاس سناریویی است که در آن تعداد مشاهدات متعلق به یک کلاس بهطور قابلتوجهی کمتر از متعلقات کلاسهای دیگر است. برای مثال، این مشکل در سناریویی برجسته است که ما نیاز به شناساییِ بیماریهای خاص، تراکنشهای تقلبی در بانک و غیره را داریم.
مثالی از کلاسهای نامتعادل
بگذارید نمونهای از دادههای تشخیص تقلب را برای درک مفهوم کلاس نامتوازن در نظر بگیریم –
کل مشاهدات = 5000
مشاهدات تقلبی = 50
مشاهدات غیر تقلبی = 4950
نرخ رویداد = 1%
راهحل
متوازن کردن کلاسها بهعنوان راهحلی برای کلاسهای نامتوازن عمل میکند. مقصود اصلی متوازنسازی کلاسها، یا افزایش فرکانس کلاس اقلیت است یا کاهش فرکانس کلاس اکثریت. در زیر رویکردهای حل مشکل عدم توازن آمده است –
نمونهبرداری مجدد[7]
نمونهبرداری مجدد مجموعهای از روشهایی است که برای بازسازی نمونه دیتاستها مورداستفاده قرار میگیرد. هم برای مجموعه آموزش دادن[8] و هم برای مجموعه آزمایشی.[9] نمونهبرداری مجدد برای بهبود دقت مدل انجام میشود. در زیر چند روش (تکنیک) نمونهبرداری مجدد آمده است –
1. نمونهبرداری تصادفیِ Under Sampling[10]
این تکنیک با هدف توازن توزیع کلاس با حذف نمونههای کلاس اکثریت بهطور تصادفی انجام میشود. این کار تا زمانی که نمونههای کلاس اقلیت و اکثریت متوازن نباشد، انجام میشود.
کل مشاهدات = 5000
مشاهدات تقلبی = 50
مشاهدات غیر تقلبی = 4950
نرخ رویداد = 1%
در این حالت ما 10% نمونه را، بدون جایگزینی در موارد غیر تقلبی میگیریم و سپس آنها را با نمونههای تقلبی ترکیب میکنیم –
- مشاهدات غیرتقلبی پس از نمونهبرداریِ تصادفی Under Sampling= 10% از 4950 برابر با
495 - کل مشاهدات پس از ترکیب آنها با مشاهدات تقلبی = 495 + 50 برابر با
545 - ازاینرو اکنون، نرخ رویداد برای دیتاست جدید بعد از نمونهبرداری تصادفی Under Sampling برابر است با 9%
مهمترین مزیت این روش این است که میتواند زمان اجرا را کاهش داده و فضای ذخیرهسازی را بهبود بخشد. اما از طرف دیگر میتواند ضمن کاهش تعداد نمونههای دادههای آموزشی، اطلاعات مفیدی را دور بیندازد.
2. نمونهبرداری تصادفیِ Over Sampling[11]
این تکنیک باهدف توازن توزیع کلاس با هدف افزایش تعداد نمونههای کلاس اقلیت از طریق تکرار آنها عمل میکند.
کل مشاهدات = 5000
مشاهدات تقلبی = 50
مشاهدات غیر تقلبی = 4950
نرخ رویداد = 1%
درصورتیکه ما 50 مشاهده تقلبی را 30 بار تکرار کنیم سپس مشاهدات تقلبی بعد از تکرار مشاهدات کلاس اقلیت، 1500 خواهد شد و بعد کل مشاهدات در دادههای جدید پس از نمونهبرداری، 1500 + 4950 برابر با 6450 خواهد بود. ازاینرو نرخ رویداد برای دیتاست جدید 6450 / 1500 برابر با 23% خواهد بود. مهمترین مزیت این روش این است که هیچگونه از دست دادنِ اطلاعات سودمندی وجود نخواهد داشت. اما از طرف دیگر شانس over-fitting را افزایش میدهد زیرا رویدادهای کلاس اقلیت را تکرار میکند.
تکنیکهای گروه
این روش اساساً برای اصلاح الگوریتمهای طبقهبندی موجود استفاده میشود تا آنها را برای دیتاستها نامتوازن مناسب سازد. در این روش چندین طبقهبندی کننده دومرحلهای از دادههای اصلی ایجاد میکنیم و سپس پیشبینیهای آنها را جمع میکنیم. طبقهبندی کننده جنگل تصادفی نمونهای از طبقهبندی کننده مبتنی بر گروه است.
بخشهای دیگر مقاله را از لینکهای زیر بخوانید:
هوش مصنوعی با پایتون – بخش پنجم – یادگیری نظارتشده : طبقهبندی (قسمت اول)
هوش مصنوعی با پایتون – بخش پنجم – یادگیری نظارتشده : طبقهبندی (قسمت دوم)
هوش مصنوعی با پایتون – بخش پنجم – یادگیری نظارتشده : طبقهبندی (قسمت سوم)
هوش مصنوعی با پایتون – بخش پنجم – یادگیری نظارتشده : طبقهبندی (قسمت چهارم)
هوش مصنوعی با پایتون – بخش پنجم – یادگیری نظارتشده : طبقهبندی (قسمت پنجم)
[1] True Positive
[2] True Negative
[3] False Positive
[4] False Negative
[5] Accuracy
[6] Specificity
[7] Re – Sampling
[8] Training Set
[9] Test Set
[10] Random Under Sampling
[11] Random Over Sampling
